Reliability Calculations in Excel

In Operations Management today we used Excel to calculate product reliability. Reliability is defined as "the ability of a product, service, part, or system to perform its intended function under a prescribed set of circumstances" (Stevenson, 2009). In order to calulate reliability over a given length of time we need to use the following formula:

P(no failure) = e-t/MTBF

where:

e = 2.7183
t = Length of service before failure
MTBF = Mean Time Between Failures

One of the cases we did in class involved an auto detailing company that wanted to calculate the reliability of its vacuum cleaners. Excel provides an "EXP" funtion that we can easily apply here. After entering all data for the problem as shown on the spreadsheet below, we type the formula =EXP(-A5/$B$2) in cell B5 and copy down. Next we plot the distribution for t=0 to the maximum life expectancy of 20 years using a line graph. What we end up with looks like a classic case of "exponential decay"...



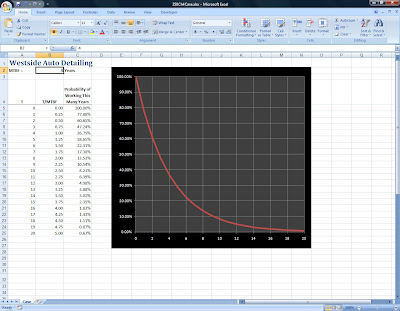
Based on this this information, we can answer questions such as what is the probability that any one of these vacuums will:

Last one year? (Answer: 77.88%)

Last four years? (Answer: 36.79%)

Fail before four years? (Answer: 1-36.79% = 63.21%)

Last between two and five years? (Answer: 60.65%-28.65% = 32.00%)

Comments

Post a Comment

Popular posts from this blog

EOQ Calculations in Excel

Image
Last week in Operations Management we used Excel to calculate the Economic Order Quantity and graph Carrying Costs, Ordering Costs, and Total Costs. The Economic Order Quantity or "EOQ" is the order size that "minimizes" Total Costs. Any more or less and you are spending too much on ordering or too much on keeping inventory. For example, in the Excel spreadsheet below, if you had an Annual Demand of 12000 units, Ordering Costs of $10 per order, and Holding costs of $4 per unit per year, the EOQ would be 245 units and Total Costs would be $980.00: We used the following formula in Excel to calculate EOQ: =SQRT((2*B2*B3)/B4) And the following formula to calculate Total Costs at this point: =$B$6/2*$B$4+$B$2/B6*$B$3 To create the graph, we used the following formulas and simply copied them over a range of 100 to 500 units. Ordering Costs: =$B$2/D2*$B$3 Holding Costs: =D2/2*$B$4 Total Costs: =F2+G2 Looking at this chart, we can clearly see that our order size of 245 is
Read more

“How Are We Doing?” Efficiency, Utilization, and Productivity

Image
In business, knowing how we are performing in relation to our competition is vital. Internally we want to know if we are using resources effectively and getting the most out of what we have. Efficiency and Productivity are two calculations that are fundamental to the success of any organization. While the calculations are simple, choosing what measures to use and collecting the necessary data requires a thorough understanding of your industry. To calculate Efficiency you will have to first decide what to use as a base for comparison. Does your company already have a “target” of some kind? Like total units produced? If so then you can compare everything to that. Once you have that, there are a couple of basic formulas that can be used: Efficiency = Actual Output/Effective Capacity X 100% Utilization = Actual Output/Design Capacity X 100% Design Capacity is the maximum output achieved under ideal conditions. Effective Capacity is always less than Design Capacity because of factors
Read more